NU Learning Phase Two:
CONFIRM
An Individual Local Treatment Difference (LTD) is an effect-size estimate within a cluster (block) of experimental units (patients) relatively well-matched in baseline-covariate X-space. The corresponding Observed LTD Distribution of effect-sizes across clusters is then either Homogeneous (purely random, highly unpredictable except in mean-effect and variance) or else Heterogeneous (at least partially predictable from patient baseline X-characteristics.) Actual prediction of LTDs (to establish Heterogeneity) is typically the stretch-goal of NU Learning Phase Four: REVEAL analyses.
The goal in NU Learning Phase Two: CONFIRM strategy is simply to establish that "X-matching Matters!" I.E., this strategy makes only relatively "fair" apples-to-apples and oranges-to-oranges comparisons. Specifically, this objective is to show that the Observed LTD Distribution from K clusters of sizes N1, N2, ..., NK differs in clearly visible and important ways from the corresponding NULL distribution that uses RANDOM subgroups (that include relatively "unfair" apples-to-oranges comparisons) under the ASSUMPTION that patient X-Covariates are IGNORABLE.
This NULL LTD distribution can be simulated to arbitrary precision by randomly permuting treated (t=1) and control (t=0) patients across the same number of clusters, of the same sizes, as the given clustering. Technically, a single random permutation of "Cluster ID Labels" across all N = N1 + N2 + ... + NK patients produces a set of K "random" LTD estimates. A total of R such independent replicates are merged to depict the full simulated random NULL distribution.
By making only the most clearly relevant X-variable comparisons, the observed LTD distribution will be relatively UNBIASED ...unless key unmeasured confounders exist.
If the observed LTD and random NULL LTD distributions are NOT clearly different, essentially nothing "interesting" has been accomplished by the current NU clustering!
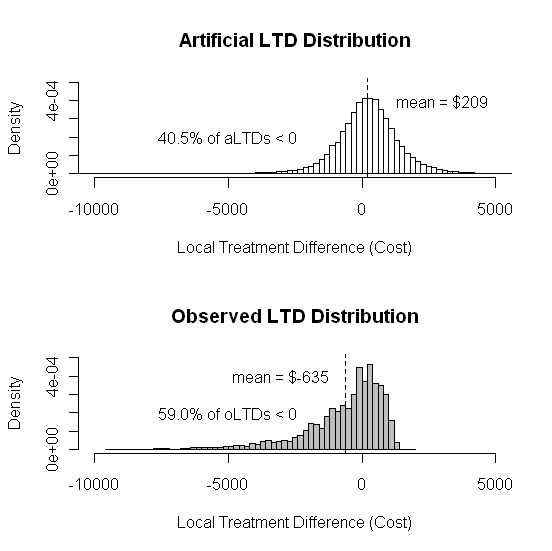
EXAMPLE: NU Learning "Confirm" graphic for 39,585 MDD Patients

Note that the top random NULL LTD distribution has a positive mean value and is essentially symmetric. In stark contrast, the observed LTD distribution has a negative mean value (an average savings of $635 per year on the New Treatment) and is highly skewed ...with a very long, left-hand tail highly favorable to the new treatment.
A formal statistical comparison of empirical Cumulative Distributions Functions (eCDFs) for the Observed LTD and random NULL distributions can be based upon the permutation distribution of the Kolmogorov-Smirnov D-statistic. However, a second set of R independent, full replications is needed because there are MANY within-cluster "ties" between random LTD estimates. The comparison below uses R = 100 replications.
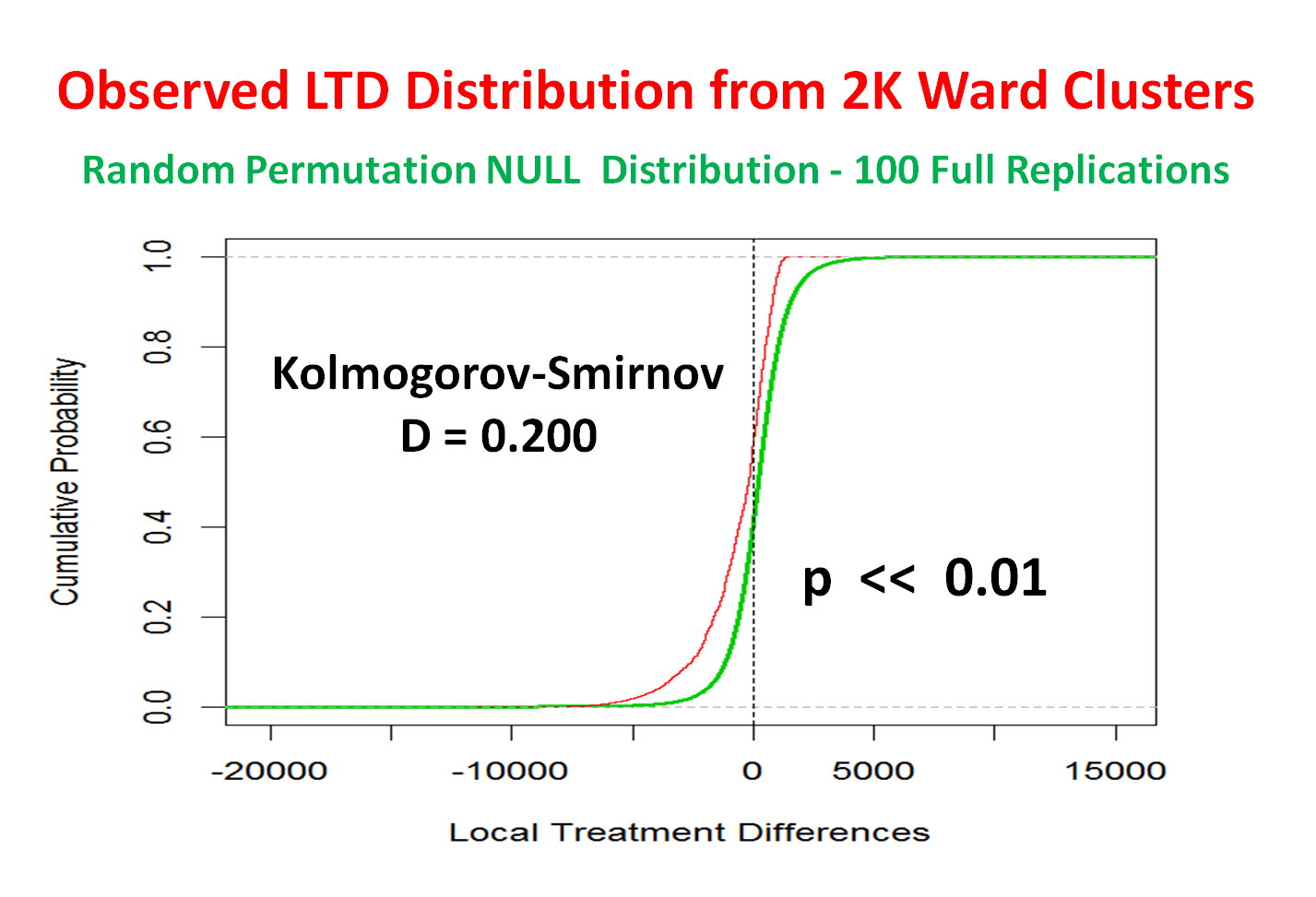
For more detail on this example, see Obenchain and Young (2013) Journal of Statistical Theory and Practice 7: 456-469.
When the observed LTD effect-size distribution appears quite similar to its homogeneous NULL distribution, observed local effects are best summarized by their global Average Treatment Effect (ATE); a traditional one-size-fits-all treatment policy is then justified.
In stark contrast, when the LTD distribution appears quite heterogeneous (as in the above example), it provides objective support for Individualized Medicine.
Guidelines for Interpretation of NU Learning Confirm Phase Graphics (6-page PDF). View/Download