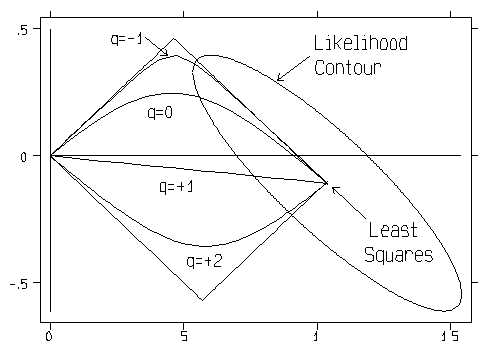
The display below shows a variety of shrinkage path Q-shapes for the rank(X) = p = 2 case.

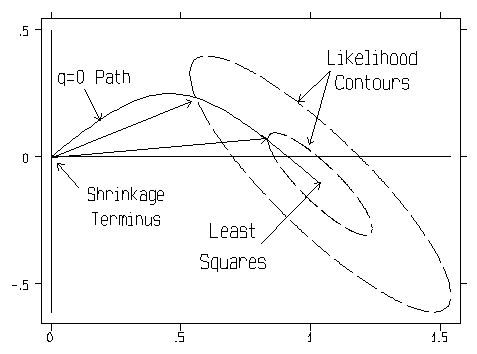
The best known special case of a Q-shaped path is probably Q = 0 for Hoerl-Kennard(1970) "ordinary" ridge regression. This path has a dual "characteristic property," illustrated in the figure below. Namely, the Q = 0 path contains not only the shortest b-vector of beta coefficient estimates with any given Residual Sum-of-Squares [RSS] but also the smallest RSS = (y - Xb)'(y - Xb) for any given b-vector length.
Another well known special case of a Q-shaped path is Q = +1 for uniform shrinkage. The coefficient TRACE and shrinkage factor TRACE for this path are both rather "dull," but the estimated risk and inferior direction TRACES can still be quite interesting even when Q = +1.
An extremely important limiting case is Q = minus infinity for principal components regression. [Marquardt(1970) calls this limit "assigned rank" regression.] My experience is that the Q = -5 path is frequently quite close, numerically, to this limiting case. Note in the top figure on this page that the path with Q = -1 shape is already near the limit in the p = 2 dimensional case being depicted here.
As a general rule-of-thumb, paths with Q-shapes in the [-1,+2] range generally tend to be fairly smooth ...i.e. have "rounded" corners. Paths with Q-shapes greater that +2 or less than -1 can display quite "sharp" corners. In fact, the paths with limiting shapes of +/- infinity are actually linear splines with join points at integer MCAL values!
My computing algorithms provide strong, objective guidance on the choice of the Q-shape that is best for your data. For example, they implement the methods of Obenchain(1975b, 1981, 1997a) to identify the path Q-shape (and the MCAL-extent of shrinkage along that path) which have maximum likelihood (under a classical, fixed coefficient, normal-theory model) of achieving overall minimum MSE risk in estimation of regression coefficients.