[2] Two Sources of ICE Uncertainty
When comparing two treatments (T vs S) on both effectiveness and cost, it is essential to have data from a sample of patients on treatment T as well as comparable data from a sample of patients receiving treatment S. When treatment "cross-over" is ethical (usually, when the underlying disease condition is chronic), these two samples of data can come from the same patients. This latter situation is much easier to treat (by forming individual differences on cost and effectiveness) but is not common; most curable disease states are acute rather than chronic.
The endogenous, statistical uncertainty within two samples of data about what could be the unknown, true overall average differences due to treatment choice is intrinsic to scientific ICE inference. This uncertainty can be directly addressed using a wedge-shaped bivariate confidence region ...a natural extension of a (univariate) confidence interval to two-dimensional (cost and effectiveness) data ...that has (0, 0) as a limit point (never as an interior point) of the region. From this purely statistical perspective, Lambda is little more than an unimportant nuisance parameter because the resulting confidence wedge is equivariant (commutative) under changes in Lambda.
At the opposite extreme, traditional economic approaches (such as "net-benefit") attempt to convert ICE inference into a univariate problem by first converting effectiveness differences into measures of cost (or utility.) Unfortunately, this introduces a second, external source of uncertainty ...about choice of Lambda... and, thus, about what might be a "fair" way to do the effectiveness-to-cost conversion! This additional exogenous uncertainty applies to all potential treatment comparisons and really needs to be kept separate and treated differently from the statistical uncertainty intrinsic to a specific (T vs. S) treatment comparison.
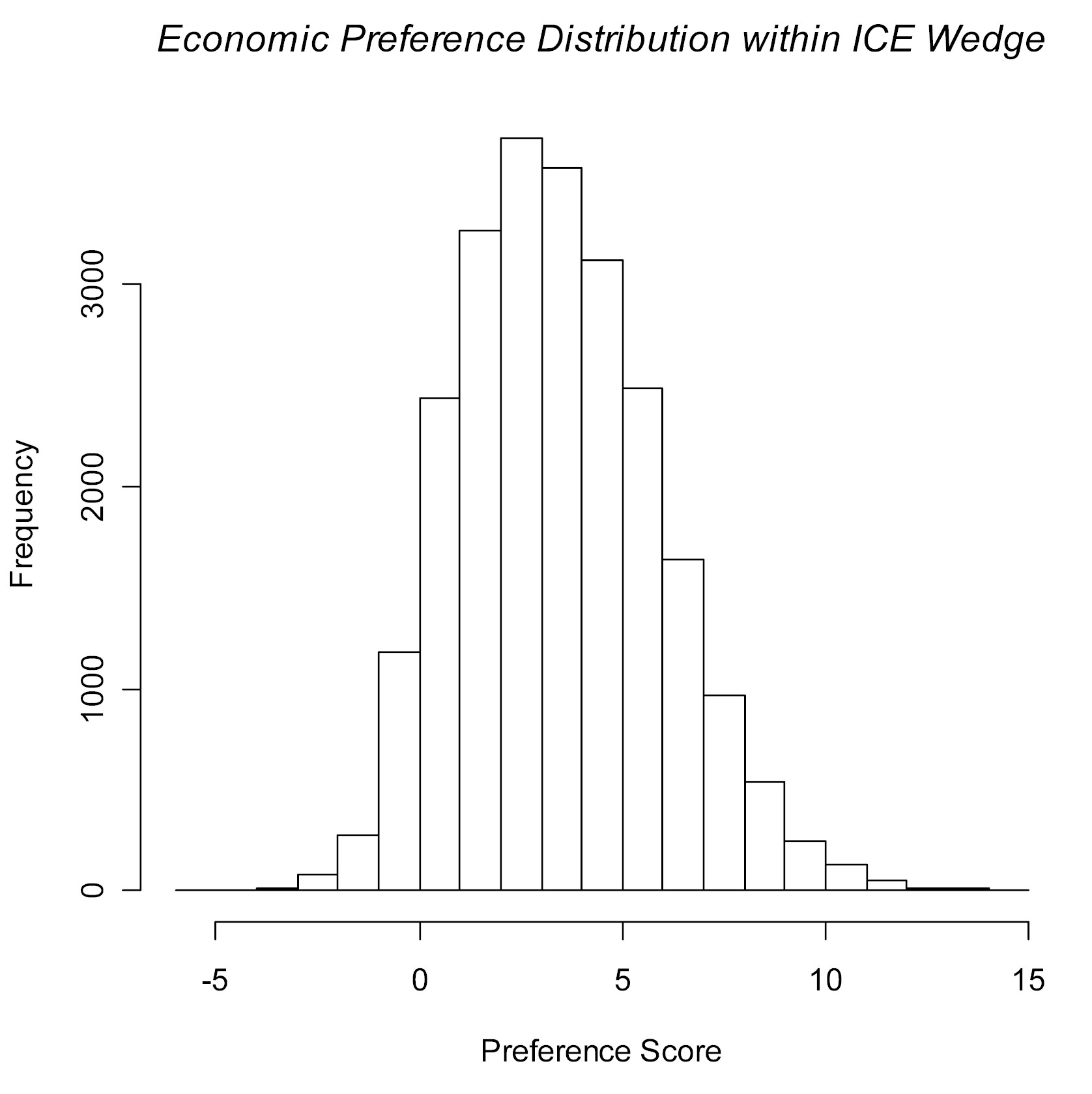
Implied Linear NB Preference Distribution when Lambda = 0.26

More Favorable? Linear NB Preference Distribution when Lambda = 2.6 NO!!!
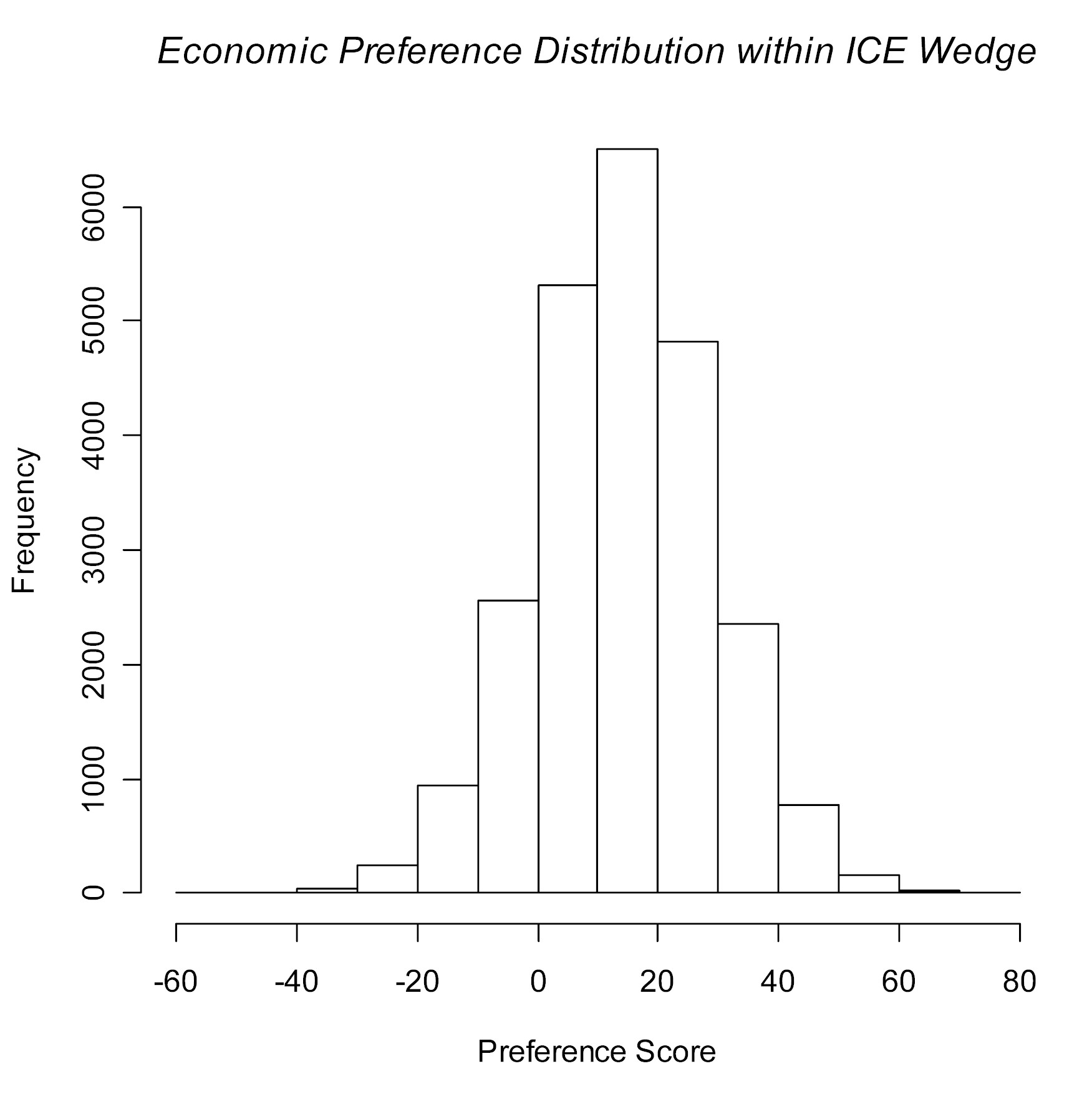
The second histogram above, for Lambda = 2.6, has a bigger and longer Negative, Left-Hand Tail than the first one for Lambda = 0.26. In other words, while the larger numerical value for Lambda does assign higher, positive numerical preference values to some bootstrap ICE uncertainty outcomes within the NE quadrant, it also assigns many less positive numerical scores to more bootstrap outcomes within the SW quadrant!!! Anyway, it is now clear that (due to injection of exogenous, economic uncertainty and inconsistency), using a larger numerical value for Lambda does not automatically produce a comparison more favorable to the new treatment, T.
Obenchain(2008) discusses graphical ways to literally "see" distinctions between these two alternative sources of uncertainty and, ultimately, to eliminate economic uncertainty about Lambda by keeping its value held fixed.