
[6] ICE Willi-Warp
See O'Brien BJ, Gertsen K, Willan AR, Faulkner LA. [Is there a kink in consumers' threshold value for cost-effectiveness in health care? Health Econ 2002; 11(2): 175-180] for background information and a discussion of Bernie O's "KINK":
WTP < WTA
This key observation states that consumers' Willingness-to-Pay (more to get more benefit) is always less than their Willingness-to-Accept (less benefit to save money.) The earlier work on "Net Benefit" by Stinnett AA, and Mullahy J. [Net health benefits: a new framework for the analysis of uncertainty in cost-effectiveness analysis. Med Dec Making, Special Issue on Pharmacoeconomics 1998; 18: S68-S80] is thus clearly rather unrealistic. In fact, Net Benefit uses the "linear" ICE preference map, NB(x, y) = x minus y, which assumes that:

See equation (5) of Obenchain RL. [ICE Preference Maps: Nonlinear Generalizations of Net Benefit and Acceptability. Health Services and Outcomes Research Methodology 2008; 8: 31-56] for Bob O's "LINK" function:
The LINK function generalizes all earlier work in the sense that it allows for cases where WTP < WTA or WTP = WTA and even (unrealistic) cases where WTP > WTA. In fact, equation (4) of Obenchain(2008) states that:
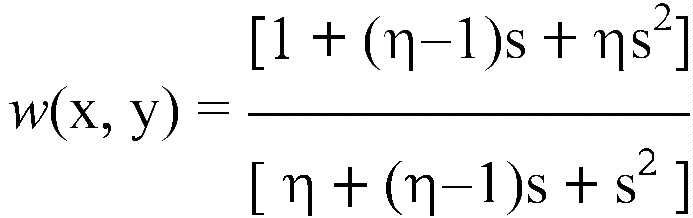
where w(x, y) is a "standardized" willingness of WTP / Lambda within the NE quadrant or WTA / Lambda within the SW quadrant, where s = y/x is the standardized ICE ratio and where Eta = Gamma / Beta is the map “power-parameter ratio.” This relationship assumes that w(x, y) is the derivative (SLOPE) of the curved, constant ICE preference contour @ (x, y) that passes through this point and, as a result, can be represented graphically as follows:
ICE Diagonal Symmetry
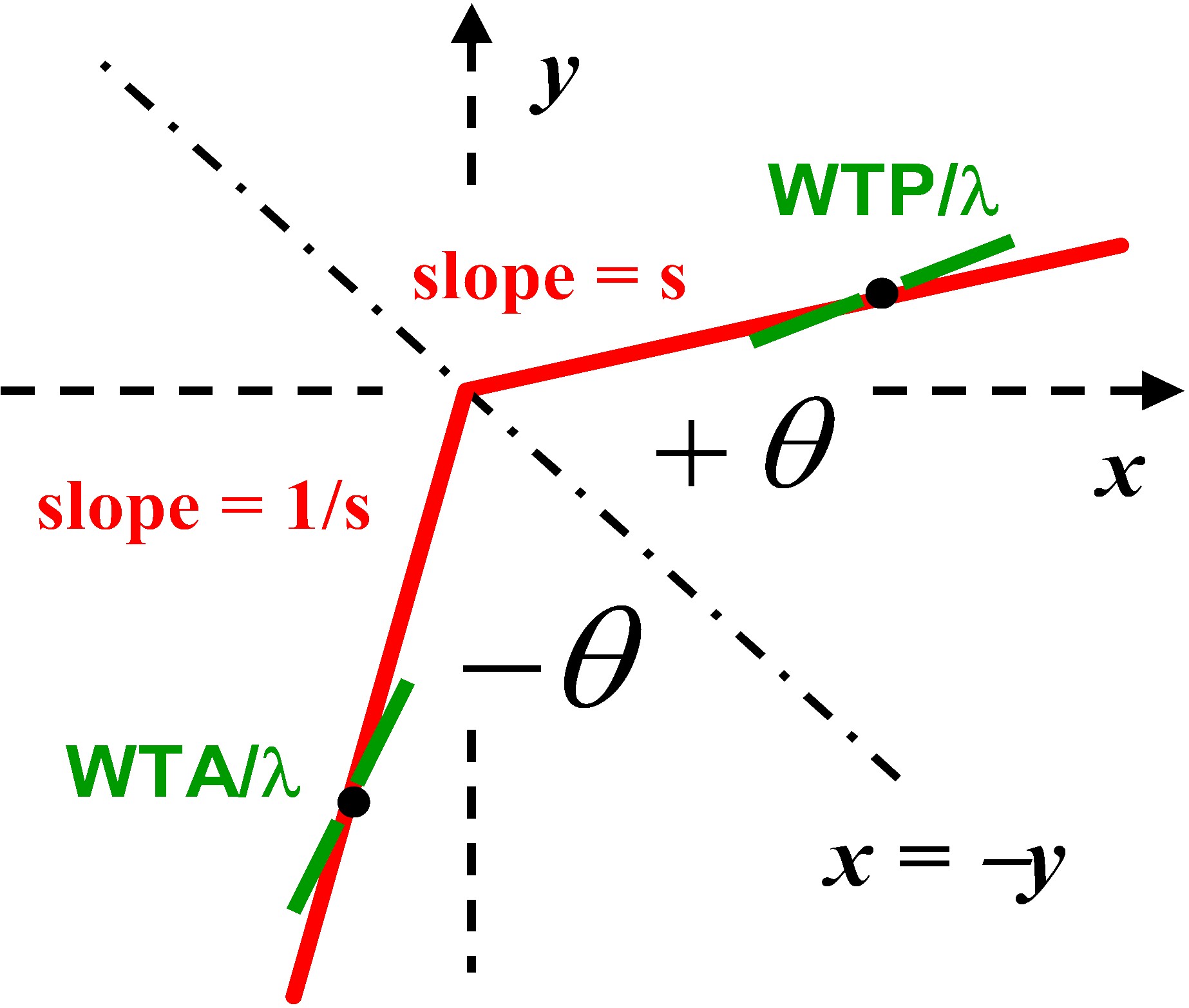
Note that the absolute ICE angle, +theta, above is 45 degrees + ArcTan(s). Thus, as s increases from 0 to infinity
(an infinite range) within the North-East ICE quadrant, theta increases only from +45 degrees to +135 degrees.
The above graphic displays a pair of standardized “dual rays” that [i] contain the same distributions of ICE preferences (varying as a function of ICE radius), [ii] correspond to equal absolute ICE polar angles relative to the upper-left to lower-right (x = -y) diagonal, and [iii] have both standardized slopes (s = y/x) and standardized willingnesses (w = WTP / Lambda or WTA / Lambda) at identical radii that are numerical reciprocals. The case depicted here corresponds to 0 < s < w < 1 < 1/w < 1/s because the "power parameter ratio" (Eta = Gamma / Beta) of the corresponding ICE preference map is greater than one (realistic.)
Equation (1) of Obenchain(2008) introduces the corresponding 2-parameter family of potentially "nonlinear" ICE preference maps as being of the general form:
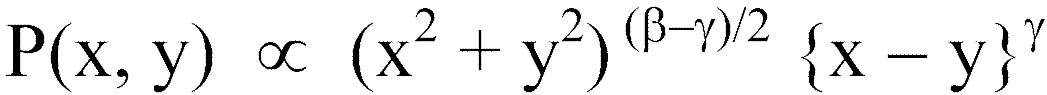
where the positive Beta "ICE radius" power determines Returns-to-Scale and the positive Gamma "signed ICE angle" power determines map "directionality." Specifically, when Gamma < Beta , the map tends to be somewhat "roundish" and quite unrealistic in the sense that WTA < WTP below the x = y (lower-left to upper-right) diagonal (ICE angle theta = +90 or -90 degrees):
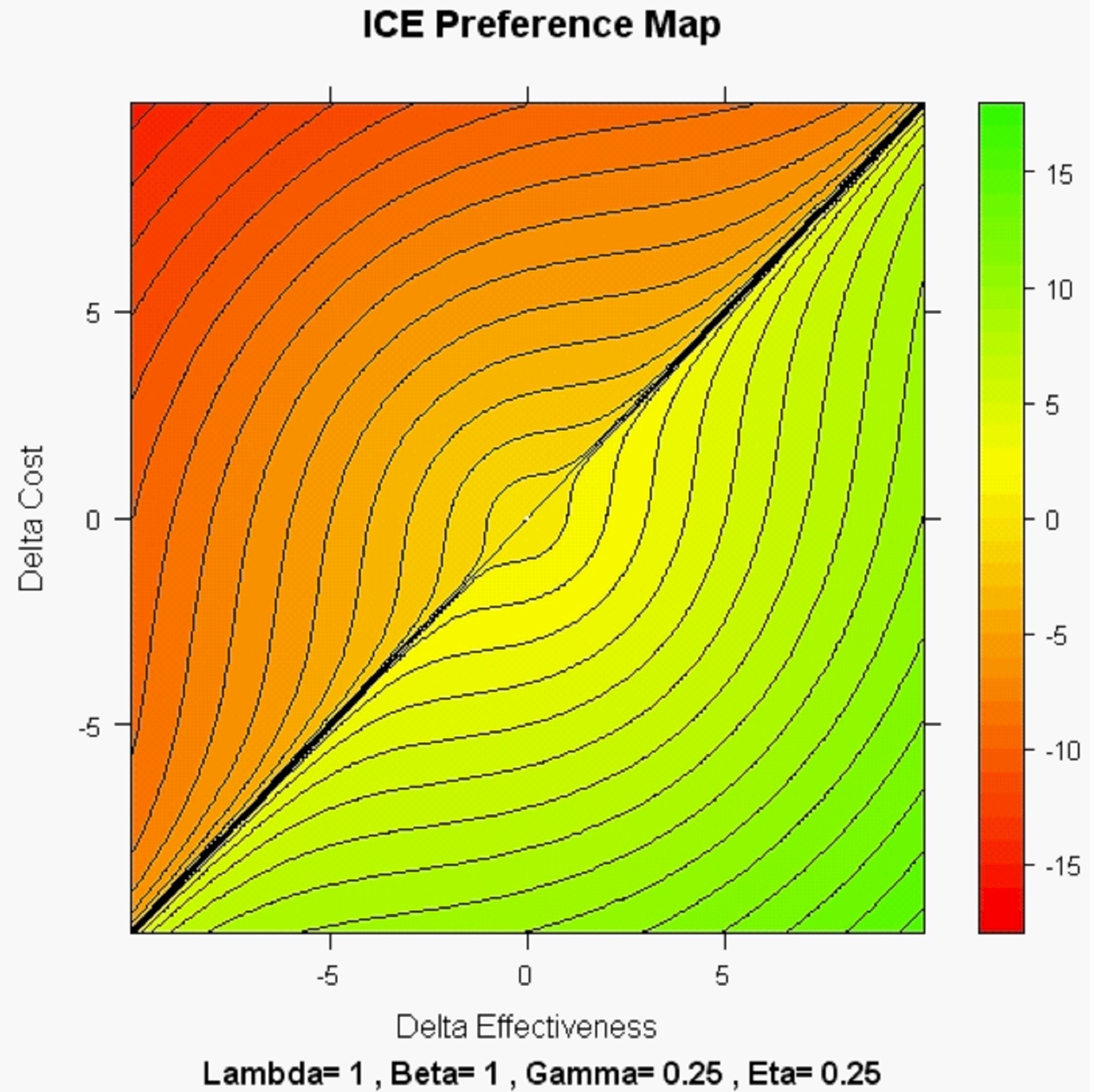
On the other hand, when Beta < Gamma, the resulting map tends to be "directional" and realistic in the sense that WTP < WTA below the x = y (lower-left to upper-right) diagonal:
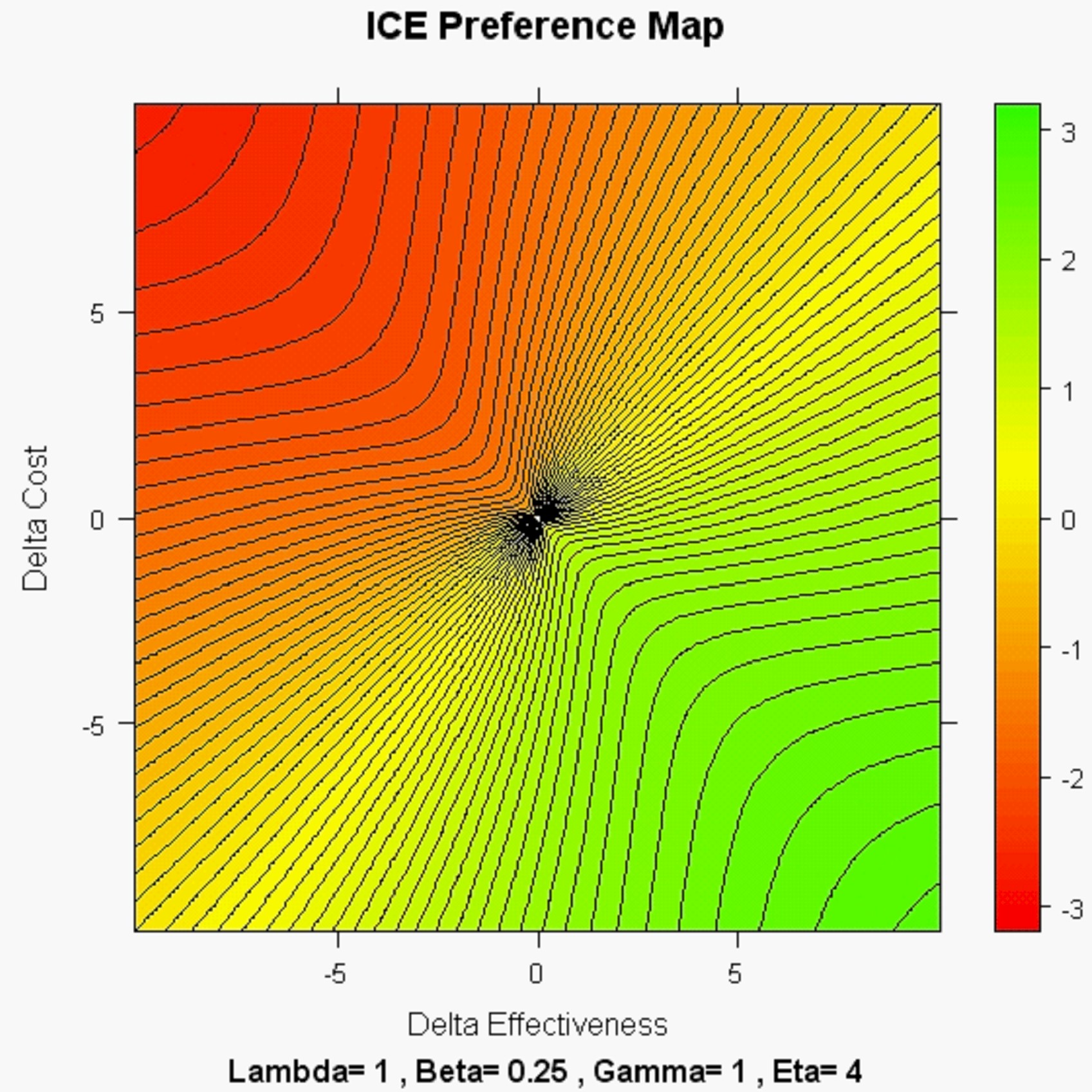
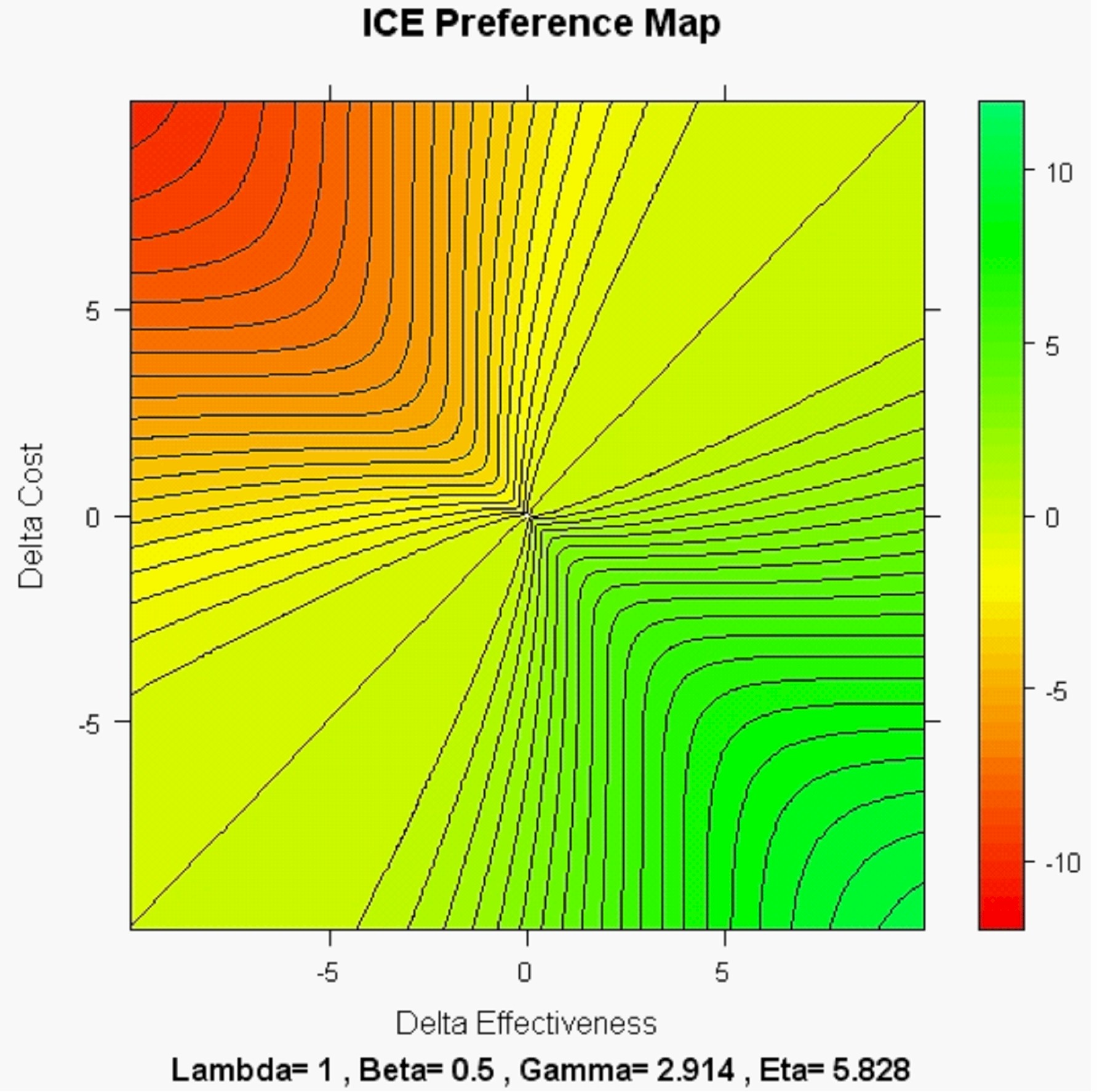
The following is an extreme map where (within the South-East ICE quadrant; ICE angle theta between +45 and -45 degrees) WTP can be as low as zero and WTA can be as high as infinity! This is a so-called "ICE Omega" map where the power parameter ratio (Eta = Gamma / Beta) assumes the maximum possible value (5.828...) consistent with the ICE monotonicity axiom.
In summary then, Bob O's "LINK" function, which states that Lambda must be the geometric mean of all well-matched WTP and WTA pairings, shows how (in the ICE Diagonal Symmetry graphic and the three non-linear ICE preference maps above) WTP and WTA can both vary between patients and societies (willi-warp) with Lambda held fixed. Specifically, when Lambda is standardized so as to always appear to be 1, as in the above ICE graphics, WTP and WTA must always appear to be numerical reciprocals: WTA = 1 / WTP.
In turn, the concept that Lambda can be meaningfully held fixed is the KEY to separating exogenous and contradictory economic uncertainty about Lambda from the endogenous statistical uncertainty in patient-level data about a specific treatment comparison (T vs. S.) In other words, Bob O's "LINK" function provides the theoretical basis for OBJECTIVELY determining Lambda for a given disease state or medical condition by eliciting well-matched pairs of WTP and WTA numerical values from patients (and their trained care givers) ...using any relevant disease-specific units of effectiveness. (The awkward and vague concepts of a QALY and of how to re-express effectiveness outcomes in QALYs then become outmoded!)