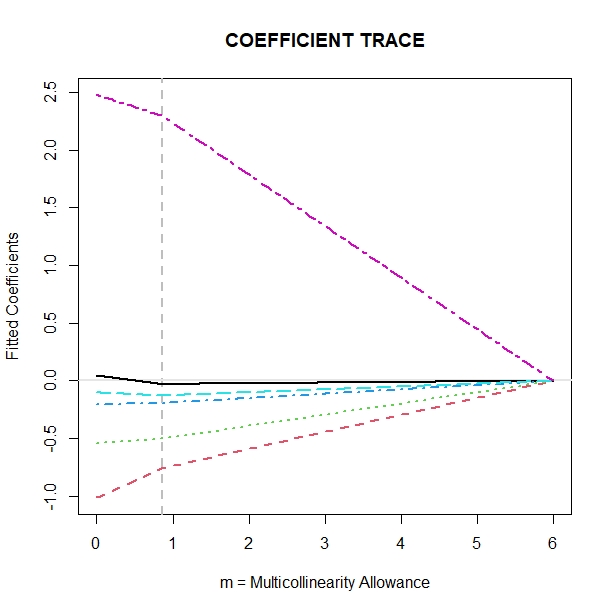
The Coefficient TRACE display below shows how the p = 6 fitted regression coefficients for the infamous Longley(1967) dataset change due to shrinkage using the (new) EFFICIENT (p = 6-parameter) PATH through Normal-theory Likelihood Space, Obenchain (2021-2022).

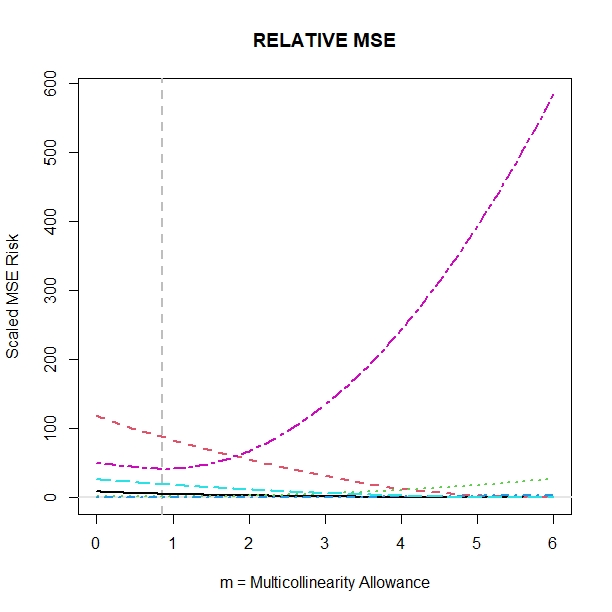
Note that just a little bit of Shrinkage of just the RIGHT FORM (above) reduces the estimated RISK (below.) When drastic reductions in Variability are combined with modest increases in Squared Bias, Overall Reductions in MSE Risk result. Note the vertical dashed-gray-lines at m = 0.86 on Both Plots that mark the overall Optimal Shrinkage m-Extent.
Information on Various GRR Topics...
softRX freeware is proud to provide computer algorithms for R and several other systems to guide you along your GRR Shrinkage "journey" Our freeware provides powerful, Maximum Likelihood statistical inferences and dynamic Xlisp-Stat graphical insights along the "Path" of your choice!